2 Convierta en radianes Exprese la respuesta en términos de π a) 30°12'30" b) 15°27'15" c) 60° d) 0° e)–300°12'12" 3 Convierta en radianes No exprese la respuesta en términos de π a) 1° b) 240° c) 3° d)75° e) 300° 4 Convierta a grados, minutos y segundos a) 1 radián b) 2 radianes c) 8π d) 12π e) 5π/4 515 Sean dos ngulos El primero mide "p" grados sexagesimales y el segundo "q" grados centesimales La diferencia numrica de estas medidas es 15 Si la suma de estos ngulos en el sistema sexagesimal es 129, los ngulos tal como estaban medidos originalmente, son a) 30 y 15 c) 60 y 45 e) 90 y 75 b) 45 y 30 d) 75 y 60 14GEOMETRÍA Y TRIGONOMETRÍA Unidad de Aprendizaje III Academia de Matemáticas 15 U A A R ZA Saberes procedimentales Saberes declarativos Traza los siguientes ángulos en un plano cartesiano e indica de que cuadrante son a) 25°, b) 75°, c) 125°, d) 135°, e) 210°, f) 235°, g) 290°, h) 30°, i) 1°, j) 280°

Todo Los Triangulos Notables Sus Angulos Medidas
Triangulo notable de 15 75
Triangulo notable de 15 75-Mostramos cómo, para ángulos agudos, las dos definiciones diferentes de las funciones trigonométricas (a partir de los catetos y la hipotenusa, y la definición a partir del círculo unitario) dan por resultado los mismos valores Creado por Sal Khan Este es= = Relaciones fundamentales 6 Si sen a = 0,28, calcula cos a y tg a utilizando las relaciones funda mentales (a < 90°)cos a = = 0,96;
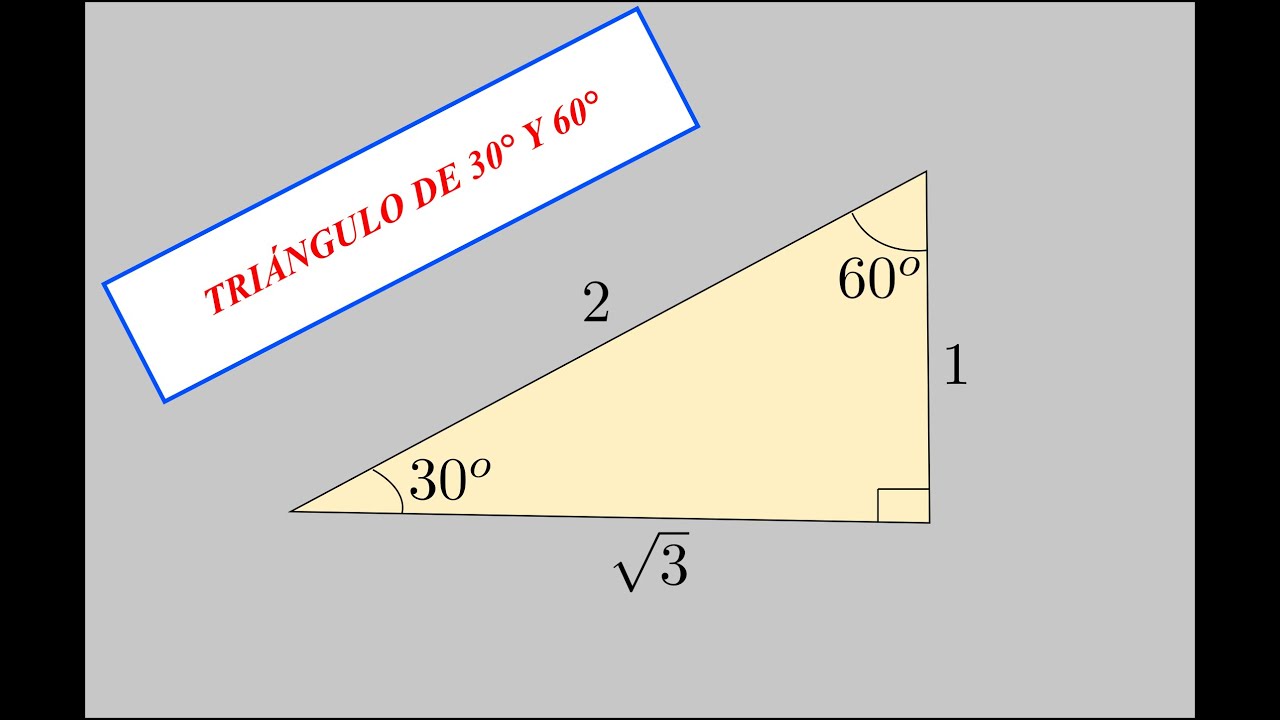



El Triangulo De 15 Y 75 Grados Youtube
Una forma fácil de obtener el seno, coseno, tangente, cotangente, secante y cosecante de los ángulos 15° y 75° Hecho por AcademiaVasquezhttps//wwwyoutubeE hipotenusa miden 8, 15 y 17 centímetros respectivamente Halle el valor aproximado (a un decimal por defecto) de seno, coseno y tangente del ángulo α Solución De acuerdo a las definiciones dadas resulta que a) senα= 8 17 ≈04 b)cosα= 15 17 ≈06 c) tgα= 8 15 ≈05 En lo que sigue estudiaremos algunas propiedades de las razonesY el mismo procedimiento se realiza para seno y coseno de 45°, a continuación se muestra una imagen con los valores exactos ya expresados Como dato, se deja aquí abajo una tabla con los valores exactos de las razones trigonométricas seno, coseno
ANGULO TRIGONOMÉTRICO Observación Es una figura generada por la rotación a) Angulo nulo de un rayo, alrededor de un punto fijo Si el rayo no gira, la medida del llamado vértice, desde una posición ángulo será cero inicial hasta una posición final 0 LF 0 b) Angulo de una vuelta Se genera por la rotación completa del rayo, es decirLos triángulos no son siempre rectos (aunque nunca son torcidos), pero cuando lo son (o sea, triángulos rectángulos), abren un apasionante mundo de posibilidades No solo los triángulos rectángulos son fascinantes en sí, también son la base de ideas muy importantes en geometría analítica (como la distancia que hay entre dos puntos en el espacio) y de trigonometríaLa ley de los senos establece que en todo triángulo, sea éste agudo, corno en la figura 1921 (A), u obtuso, como en la figura 1921 (B), es cierta la siguiente relación EJEMPLO En la figura 1921 (A) el ángulo A es de 15° y el ángulo C es de 85°
Ejemplo 1 Flujo de caja en acciones El flujo anual de efectivo en acciones (medido en porcentaje de activo totales), ha fluctuado en ciclos de unos 40 años desde 1955, cuando estaba en un punto máximo Los máximos aproximados fueron $15%$ de los activos totales, mientras que los mínimos aproximados fueron $10%$ de los activos totales*RAZONES TRIGONOMETRICAS 1 Las razones trigonométricas relacionan dos lados y un angulo en los triángulos A) Rectángulos B) obtusangulo C) Equilateros D) isosceles 2 En un triángulo rectángulo, el lado opuesto al angulo recto se llamaEncuentra una respuesta a tu pregunta Dos ángulos internos de un triángulo miden 75 y 15 calcular el tercer ángulo que tipo es el triangulo 1 Iniciar sesión Registrarse 1 Iniciar sesión Registrarse Preguntar Nahali123 Nahali123 Matemáticas Secundaria




Problemas Resueltos Tema 4 Resolucion De Triangulos 1 Triangulo Trigonometria




Ideas De Trigonometria Trigonometria Razones Trigonometricas Secundaria Matematicas
22 Calcula la longitud del lado de un pentágono regular inscrito en un círculo de diámetro 10cm 23 Calcula el perímetro y la superficie de un octágono regular inscrito en un círculo cuyo diámetro es de 5 m 24 Calcular el radio del circulo inscrito en un hexágono regular cuyo lado es de 075 m 25 Calcular el perímetro y la superficie de un rectángulo cuya diagonal mide 40Luego, calculamos las razones trigonométricas, a partir de sus respectivas definiciones y con los datos dados y obtenidos 15 sen 17 α 8 cos 17 α 15 tan 8 α 17 csc 15 α 17 sec 8 α 8 co t 15 α α 8 15 17 Razones TrigonométricasY son triángulos congruentes porque sus lados y ángulos correspondientes son iguales Veamos otro par de triángulos Abajo se muestran los triángulos y Estos dos triángulos no son congruentes porque es claramente más pequeño en tamaño que Pero, a pesar de que no tienen el mismo tamaño, se parecen el uno al otro



Q Tbn And9gctmjyoqkjmgtebgv0gxtwcbc A 5r2xji0sofv8pctelkduxcfy Usqp Cau




Trigonometria Ejercicios Y Calculo De Razones Trigonometricas Docsity
Su objeto es la medición de los ángulos y lados de untriángulo rectángulo inscrito o circunscrito en una circunferencia en cuyocentro se ha construido un sistema de coordenadas cartesianas, con elpropósito de"3 y uno de sus ángulos es de 60° Solución Primero se hace un esquema del triángulo y se identifica como se ve en la FIGURA 1012 Se desea determinar a, b y b Puesto que a son ángulos complementarios, a 1 b 5 90°, y b5 90°2a5 2 60° 5 30° La longitud de la Check Pages 101 150 of MatematicasIIGeometriatrigonometria in the flip PDF version MatematicasIIGeometriatrigonometria was published by carlos delgado on Find more similar flip PDFs like MatematicasIIGeometriatrigonometria Download MatematicasIIGeometriatrigonometria PDF for free



Www Cbtis136 Edu Mx Public Noticias D167e3c6b532f70ac4f18db11a6a4e90 Pdf




Pdf La Trigonometria En Tres Lecciones Manual Del Estudiante Jorge M Lopez Fernandez 26 De Agosto De 18
Unidad 4 Resolución de triángulos BACHILLERATO 11 Matemáticas I 7 Estrategia de la altura para resolver triángulos oblicuángulos Página 115 1 En un triángulo ABC conocemos A^ = 68°, b˜=˜172 m y a = 1 m Calcula la longitud del lado c AH = 172 cos 68° = 64,43 m CH = 172 sen 68° = 159,48 m HB = aC2 – H 2 = ,75 m C = AH HB = 64,43 m ,75 m = 154,18 m B7 Soluciones a los ejercicios y problemas 5 Calcula las razones trigonométricas de los ángulos A^ y C^, ABD ì y CBD ì = = 9;Apuntes de Pensamiento Trigonometrico Generalidades del curso Materia Pensamiento Trigonométrico Campo disciplinar Matemáticas y Razonamiento Complejo Profr Carlos Justino Arévalo García Página web del curso trigocarlosjustinowikispacescom Horario de trabajo de la materia Hora Lun Mart Miérco Juev Viern es es les es es 940 – 2




Todo Los Triangulos Notables Sus Angulos Medidas



18 Problemas Sobre Triangulos Rectangulos
Sen45°= 1 = 1 1 Así es como obtenemos el valor exacto de tangente para el ángulo de 45°;E)_La hipotenusa de un triangulo mide 17cm y el ángulo de la altura 69° Calcula la medida de la base del triangulo(c) AC = 8 BC = 15 En cada caso, use el teorema de Pitágoras para encontrar el tercer lado y luego encuentre el seno y el coseno de los ángulos A y B Está ascendiendo por un camino y ve un signo que le indica que tiene 5 grados, o sea que asciende 5 m por cada 100 m de camino
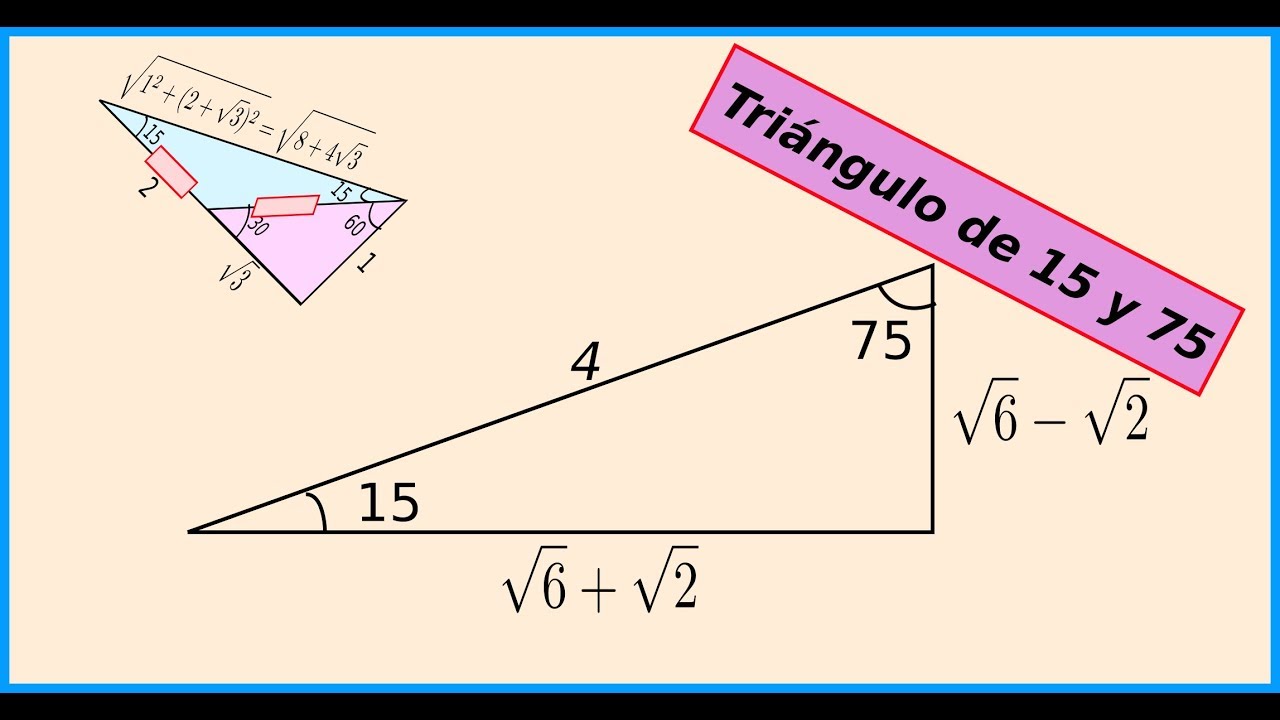



El Triangulo De 15 Y 75 Grados Youtube




Seno Coseno Tangente Ck 12 Foundation
De acordo com estas informações, a medida em metros, de um estádio era a) 15,75 b) 50,00 c) 157,50 d) 393,75 e) 500,00 Ver Resposta Alternativa c) 157,50 Veja também Fórmulas de Matemática Compartilhar Enviar Email Rosimar GouveiaAngulo Trigonométrico y Sistemas de Medidas Angulares 1 TRIGONOMETRIALa Trigonometría constituye el quinto y último nivel de Matemáticas en losestudios secundarios; Solución Primero hallamos el valor de la hipotenusa, aplicando el Teorema de Pitágoras;




Triangulos De 30 Y 60 45 Y 45 37 Y 53 Razones Trigonometricas Notables Ejercicios Resueltos Pdf
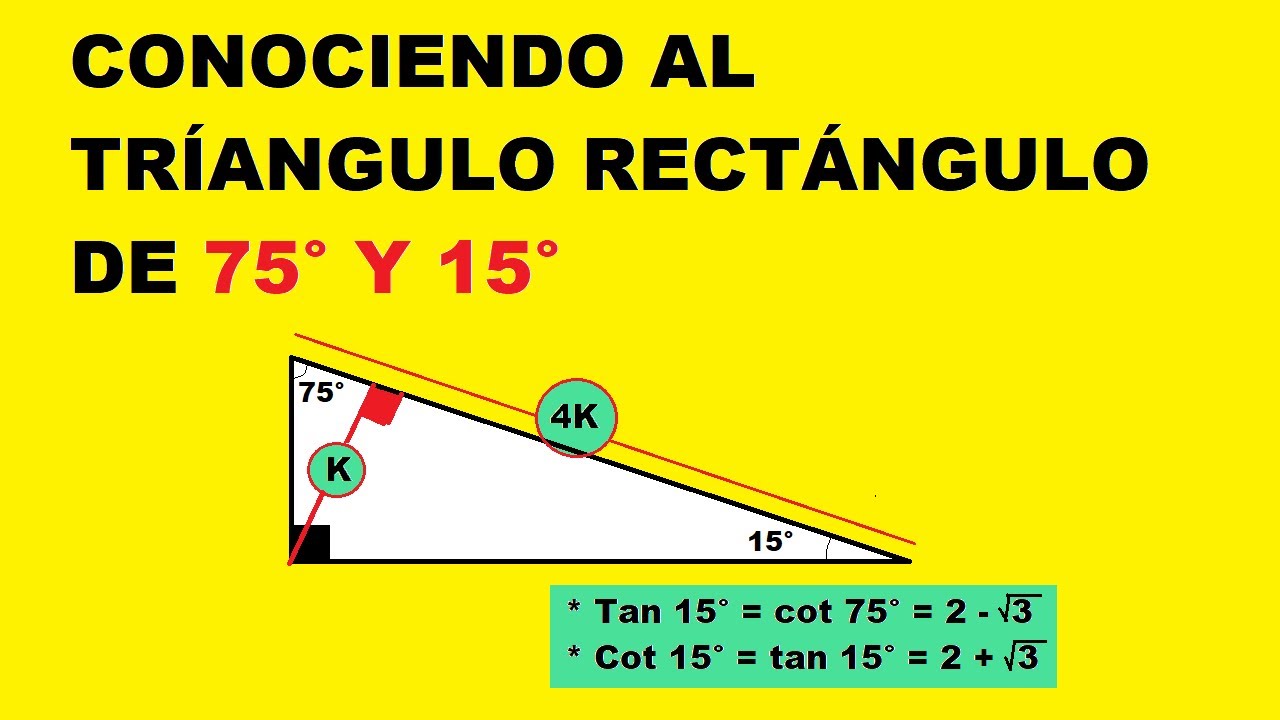



Un Interesante Triangulo Notable 75 Y 15 Conclusiones Youtube
Muestra una relación de razones entre el lado de un triangulo y su ángulo opuesto ó viceversa siendo la A=80° B=2°15´ b=81cm 2 A=42°10´ B=59°30´ a=135cm 3 A=55° C=61°37´ a=6332cm Un paralelogramo tiene lados cuyas longitudes son 32 y 75 cm y uno de sus ángulos mide 73° Calcular la longitud de sus diagonales a) Ecuación de una recta cuya pendiente es m y un punto de paso es p1(x1;y1) y – y1 = m(x – x1) b) Ecuación de una recta conociendo dos puntos de paso p1(x1,y1) y p2(x2;y2) )xx( xx yy yy 1 12 12 1 c) Ecuación de una recta cuya pendiente es m e intersección con el eje de ordenadas es (0;b) y=mxb d) Ecuación de una recta conociendoRazones en triángulos rectángulos Aprende Preparación para triángulos rectángulos y trigonometría (Abre un modal) Hipotenusa, opuesto y adyacente (Abre un modal) Razones laterales en triángulos rectángulos como función de los ángulos (Abre un modal) Utilizar semejanza para estimar la razón entre longitudes laterales




Trigonometria Preuniversitaria Cuarta Guia Resuelta Preguntas Tipo Examen De Admision A La Universidad



Prepaermilo Uacam Mx View Download File 162 Antologia de geometria y trigonometria Pdf Tipo Paginas
Ahora, ya se conocen valores exactos de las funciones seno y coseno de los ángulos 15°, 30°, 45° y 60° En base a ésta información, uno puede calcular en forma exacta, los valores de las funciones seno y coseno cada 15° Analizando el primer cuadrante, tenemos los valores exactos de 15°, 30°, 45°, 60° y 75° Hay que notar que para el Traza 10 Un triángulo isósceles tiene una base que mide 56 cm y una altura de 96 Traza 15 La diferencia entre el lado oblicuo y la base mide cm;ANALIZANDO II Para este triángulo, debemos determinar por lo menos un ángulo para poder aplicar tanto ley de cosenos como senos Para ello, encontramos el complemento de 273° δ =90 °−273° δ =8727 ° Ahora podemos aplicar ley de senos sen 8727 (130) β=sen−1 ( ) 450 β=1677 ° Por tanto, para encontrar el ángulo restante α



Www Uv Es Lonjedo Esoproblemas Unidad6trigonometria Pdf



Q Tbn And9gcsrwu7na8r5qsqei39hph1wf7g6vpc rb Tgmzjwfsp1hrf5n Usqp Cau
Razones trigonométricas de triángulos especiales Aprende a determinar el seno, coseno y tangente de triángulos y también de tríangulos Hasta ahora hemos utilizado la calculadora para evaluar el seno, coseno y tangente de un ángulo Sin embargo, es posible determinar las funciones trigonométricas de ciertos ángulosEsto es, 960 5 1 240 Entonces, este ángulo se forma dando dos rotaciones en sentido contrario al de lasUn cateto es de 7 la del cateto es 19,2 cm, calcular el área y el perímetro del triángulo Traza 75



Upload Wikimedia Org Wikipedia Commons B B4 Valores Trigonom C3 tricos Exactos De La Funci C3 n Seno Y Coseno Pdf



Matematicasiesoja Files Wordpress Com 13 10 05ii Pdf
Para más ejercicios resueltos de triángulos notables y de matemática, visita totalmente gratis los siguientes enlaceshttp//mihijoconbuenanotaenmatecom/htTangente es la función trigonométrica que aplica al ángulo α la razón entre la ordenada "y" y la abscisa "x" del punto P y Sen Tangente (α) = x Cos y Sen Tg α = x Cos 4 La Cotangente es la función inversa de la tangente, es decir y 1 Cotangente (α) = ó x tag 1 y Ctg α = x ó Ctg α = tag 5Magnitud y signo de estas últimas se pueden obtener los valores de las primeras Los valores notables de las funciones trigonométricas se obtienen a partir de sus definiciones considerando los valores de los catetos y de la hipotenusa Por ejemplo, para calcular los valores para 30 ° se puede construir la siguiente figura 2 3 2 1 2 1 30 °




Resolucion De Triangulos Superprof




49 Ideas De Razones Trigonometricas Razones Trigonometricas Trigonometria Secundaria Matematicas
Identificar las Seis Funciones Trigonométricas Objetivos de Aprendizaje Identificar la hipotenusa, el cateto adyacente y el cateto opuesto de un ángulo agudo en un triángulo rectángulo Determinar las seis funciones trigonométricas de un ángulo dado en un triángulo rectángulo Reconocer la relación recíproca entre seno/cosecante, coseno/secante, y tangente/cotangenteC)_Un avión despega formando con el suelo un ángulo de 15°, ¿cuál será la distancia sobre la pista, cuando el avión haya recorrido 1100m de vuelo desde el punto de elevación?21'75 sen25º sen50º b 12 sen50º b 7 Calcula los ángulos y el lado de un rombo de diagonales 60cm, 80cm 14 Calcula la altura h de la siguiente figura 15 Resuelve los siguientes triángulos conocidos a) ºb =cm,c =35cm, A =55 b) cma =15cm,b =25cm,c =35 c) a =cm, A =35º,B =75º




Todo Los Triangulos Notables Sus Angulos Medidas



Http Docs Uprb Edu Deptmate Material suplementario Cime 10mo a 12mo T8 3b funciones de trigom E9tricas 2810mo a 12mo 29 Pdf
El lado En un triángulo rectángulo la hipotenusa es 25 cm de largo;Función de seno y coseno Cálculo de lados y ángulos de un triángulo rectángulo, conocidos algunos de ellos Obtención de la altura de Halla las razones trigonométricas del ángulo de 75°, sabiendo que las razones de 15° son sen 15° = 0,259 cos 15° = 0,966 tg 15° = 0,268 1Tg a = ≈ 0,292 7 Halla el valor exacto (con radicales) de sen a y tg a sabiendo que




Solucion De Los Problemas Eet285 Trigonometria




Ejercicios Con Triangulos Oblicuangulos Superprof
Jesus Mendez Leer Teoría Triángulo Notable de 15° y 75° previous Razones trigonométricas de ángulos notables Parte II next Triángulo Notable de 37°/2 yA los ángulos de 30º, 45º y 60º (ó sus equivalentes en radianes π/6 rad, π/4 rad y π/3 rad) se les conoce como ángulos notablesSe llaman así porque aparecen muy a menudo en nuestra vida cotidiana, y resulta de gran utilidad aprender de memoria los valores de Triangulo de 15 y 75 grados Triángulo notable de 37/2 grados Triángulo notable de 53/2 grados Los triángulos notables más usados Los triángulos notables más importantes, por así decirlo, son aquellos que se ven con mayor frecuencia en soluciones de problemas en materias como la geometría, trigonometría, física y otros




Ejercicios Resueltos 1º Bach Resolucion De Triangulos By Fiquima Kcc Issuu




Todo Los Triangulos Notables Sus Angulos Medidas
Lo bueno, malo y feo de la capacitación a directores Jesus Mendez Leer Teoría Triángulo Notable de 15° y 75° previous Razones trigonométricas de ángulos notables Parte II next Triángulo Notable de 37°/2 y 53°/2Resuelve el triángulo de datos A = 30°, a = 3 m y b = 8 m Como el seno de un ángulo nunca puede ser mayor que 1, el problema no tiene solución La figura muestra la imposibilidad de que exista el triángulo planteado 2 sen B = 1 Solución única triángulo rectángulo Resuelve el triángulo de datos A = 30°, a = 3 m y b = 6 m81 Ángulos y sus medidas 357 Solución a) Primero se determina cuántas rotaciones completas se dan para formar este ángulo Al dividir 960 entre 360 se obtiene un cociente de 2, y un residuo de 240;




Triangulo Notable De 15º Y 75º Demostracion Youtube
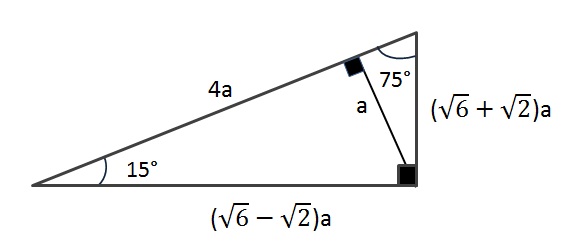



Las Razones By Nanogom4 On Emaze
Twitch https//wwwtwitchtv/matefacil Canal de Física https//wwwyoutubecom/channel/UCeFNpGn8diSNszUAKaqM_A MIRA EL CURSO COMPLETO DE TRIGONOMETRIA AQUA) 60cm B) 45cm C) 50 cm D) 75 cm 8 En una empresa se fabrica tejas especiales de techo de 30 cm de largo cuyos extremos son arcos de 4 cm de radio y ángulo central de 1°, tal y como se representa en la figura ¿A cuánto asciende el costo de producción de un millar y medio de este tipo de tejas, si el precio por metro
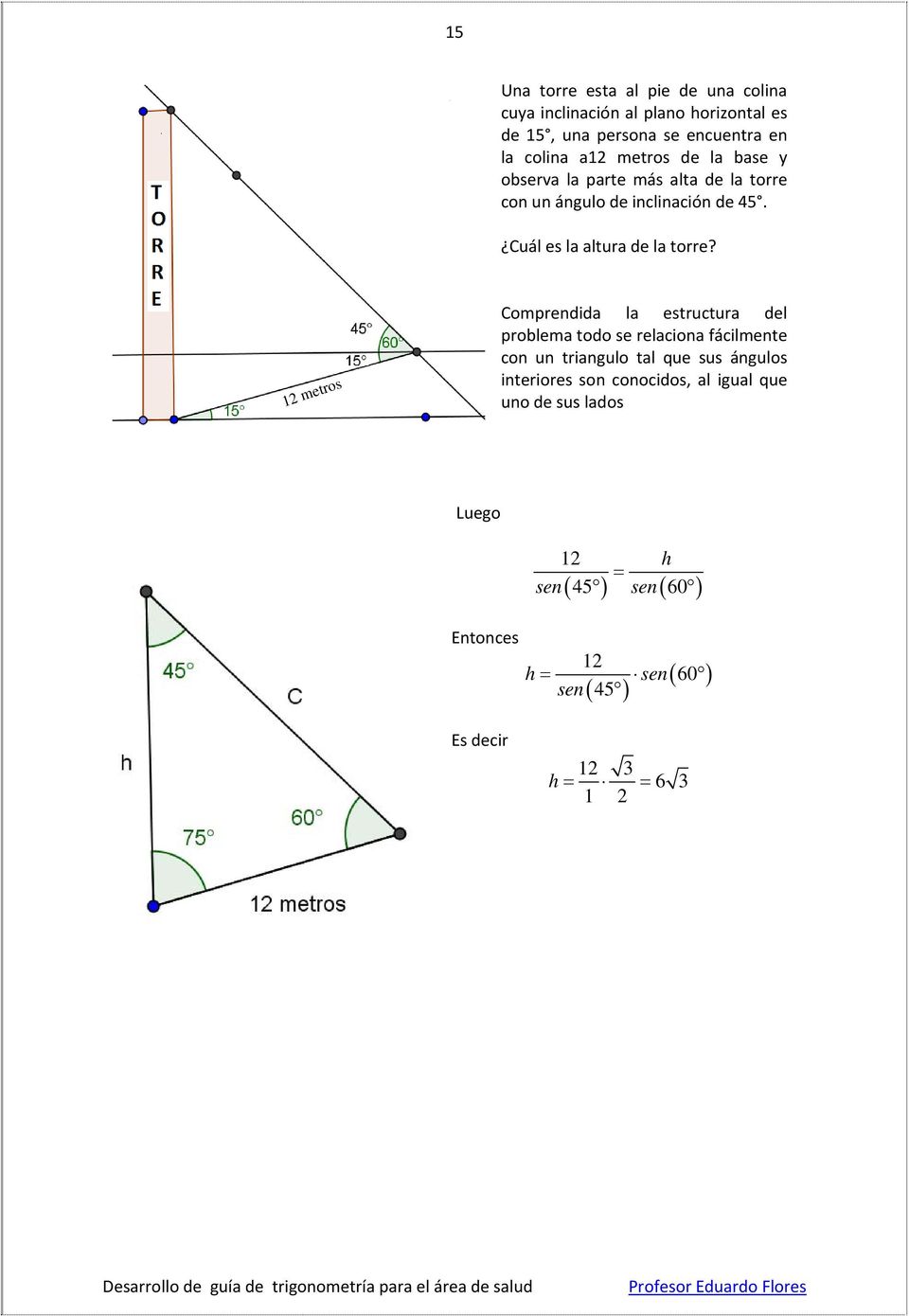



Los Catetos De Un Triangulo Rectangulo Miden 3 Cm Y 4 Cm Respectivamente Cuanto Mide El Coseno Del Menor Angulo 3 Sin A 5 4 Cos A Pdf Descargar Libre



Unidad 1 Trigonometria 1 10 Zona De Aprendizaje Matematico




Teorema Del Seno Y Coseno Superprof




Ley De Los Senos




Geometria Y Trigonometria S2 Course



Triangulos Rectangulos Y Oblicuangulos Matematica Y Listo Respuestas



Triangulos Notable Matematica Para Secundaria




Trigonometria



Www Cbtis136 Edu Mx Public Noticias D167e3c6b532f70ac4f18db11a6a4e90 Pdf



Resources Aprendoencasa Pe Perueduca Secundaria 5 Semana 14 Pdf S14 Sec 5 Solucion Matematica Dia 3 Pdf




Calameo Solucion De Triangulos Rectangulos Problemas Sobre Razones Trigonometricas 10 Segundo Corte 15




Triangulos Notables 15 75
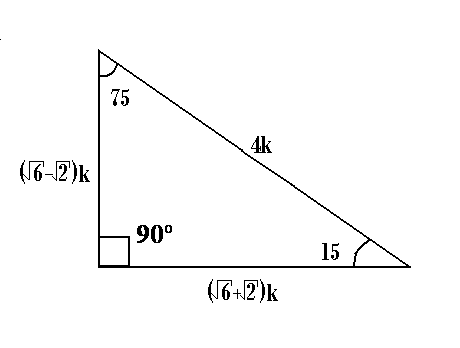



Archivo Triangulo Auxiliar De 75 Y 15 Png Wikipedia La Enciclopedia Libre




Todo Los Triangulos Notables Sus Angulos Medidas




El Triangulo De 15 Y 75 Grados Youtube
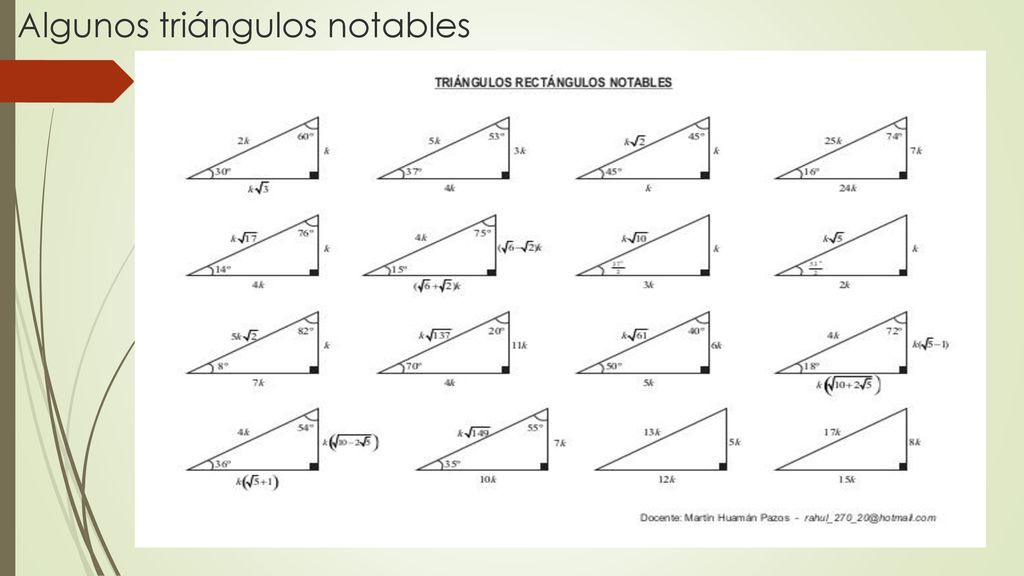



Razones Trigonometricas En El Triangulo Rectangulo Ppt Descargar




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulos Rectangulos Notables Completo




La Formula De Heron Para El Area De Un Triangulo Y Resolver Problemas Con Trigonometria Ck 12 Foundation



Www Fio Unicen Edu Ar Usuario Boucigue Apuntes Trigonometria Triangulos Funciones Pdf




Todo Los Triangulos Notables Sus Angulos Medidas



Prepaermilo Uacam Mx View Download File 162 Antologia de geometria y trigonometria Pdf Tipo Paginas




Calameo Trigonometria




Funciones Trigonometricas De Los Angulos 15 Y 75 Youtube




Bloque Ppt Descargar



Http Www Itsmante Edu Mx Wp Content Uploads 17 11 Cuadernillo De Trigonometria Pdf




Que Es Triangulos Rectangulos Notables




Todo Los Triangulos Notables Sus Angulos Medidas




Ejercicios De Trigonometria En Triangulos Rectangulo Docsity
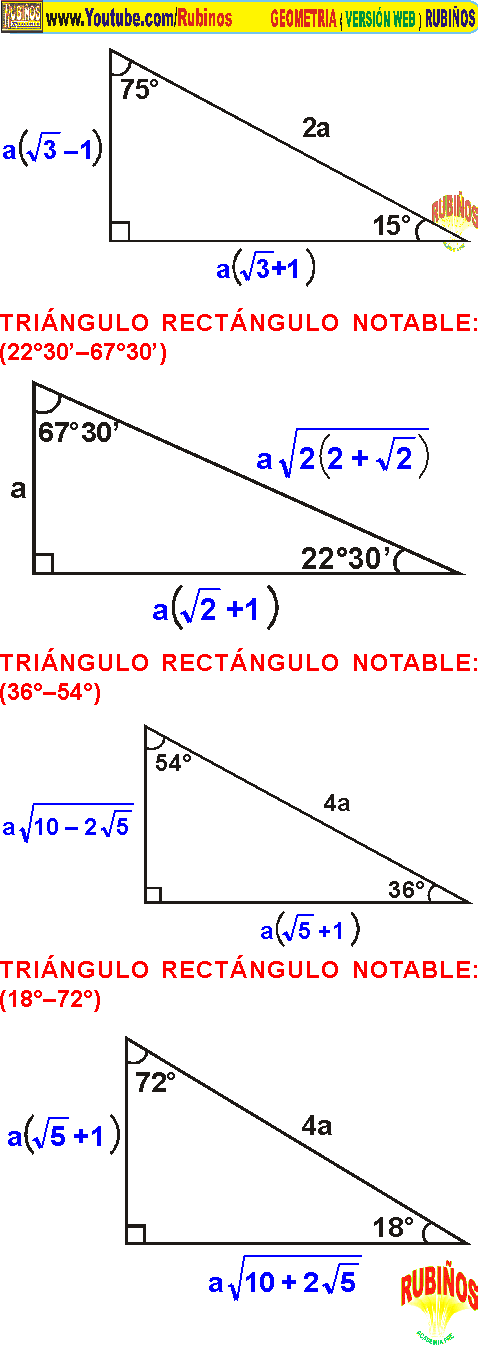



Triangulos Notables Ejercicios Resueltos Pdf



Prepaermilo Uacam Mx View Download File 162 Antologia de geometria y trigonometria Pdf Tipo Paginas



Www Fio Unicen Edu Ar Usuario Boucigue Apuntes Trigonometria Triangulos Funciones Pdf




Pdf La Trigonometria En Tres Lecciones Manual Del Estudiante Jorge M Lopez Fernandez 26 De Agosto De 18




Todo Los Triangulos Notables Sus Angulos Medidas



Http Recursostic Educacion Es Secundaria Edad 4esomatematicasa 4quincena7 Impresos 4quincena7 Pdf




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulo Notable De 15 Y 75 6 Youtube
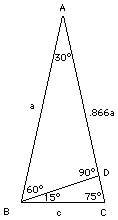



Deducir Los Senos Y Los Cosenos



Razones Trigonometricas De Un Angulo Agudo 1ºbach Wikipedia
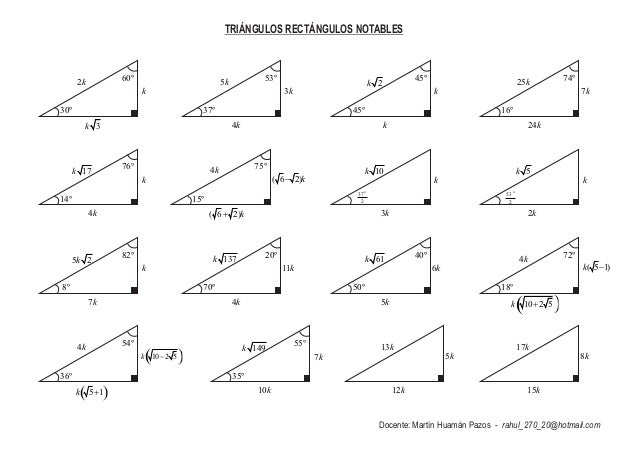



Triangulos Rectangulos Notables Completo




Triangulo Notable De 15 Y 75 Profesorajesus Com
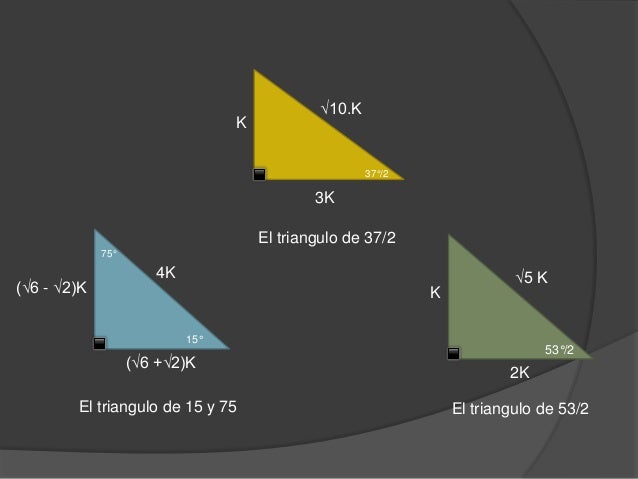



Triangulos Notables



1




50 グレア75 15 Triangulo




Todo Los Triangulos Notables Sus Angulos Medidas



Http Docs Uprb Edu Deptmate Material suplementario Cime 10mo a 12mo T8 3b funciones de trigom E9tricas 2810mo a 12mo 29 Pdf
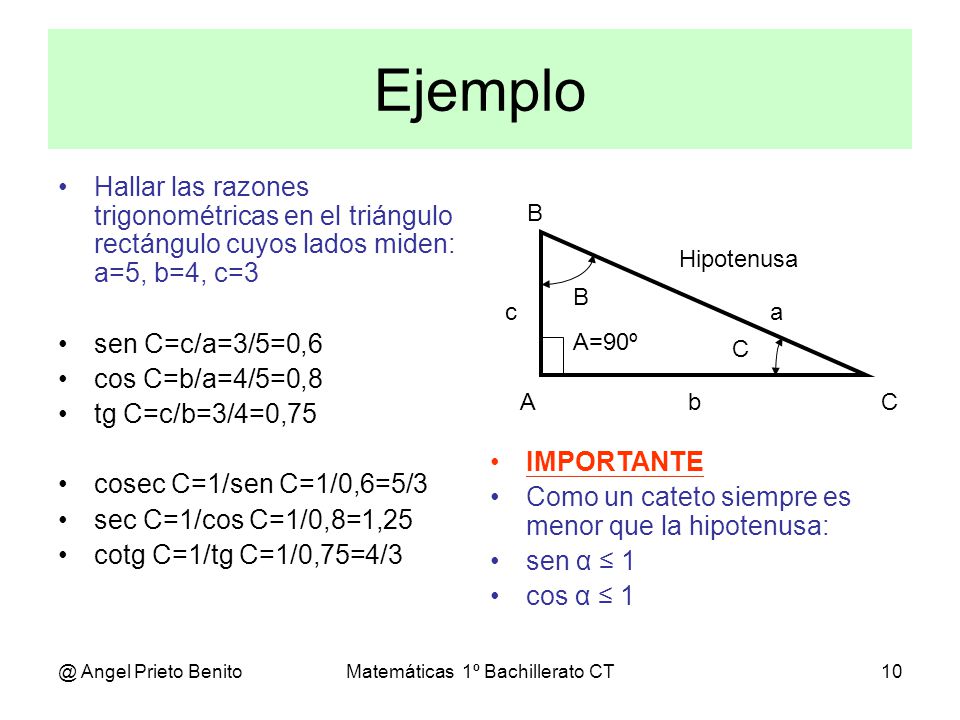



Trigonometria Dia 15 1º Bad Ct Ppt Descargar




Triangulo Rectangulo Notable De 15 Y 75 Youtube




Trigonometria Problemas De Matematicas Resueltos




Ejercicios Con Triangulos Oblicuangulos Superprof




Funciones Trigonomrtricas
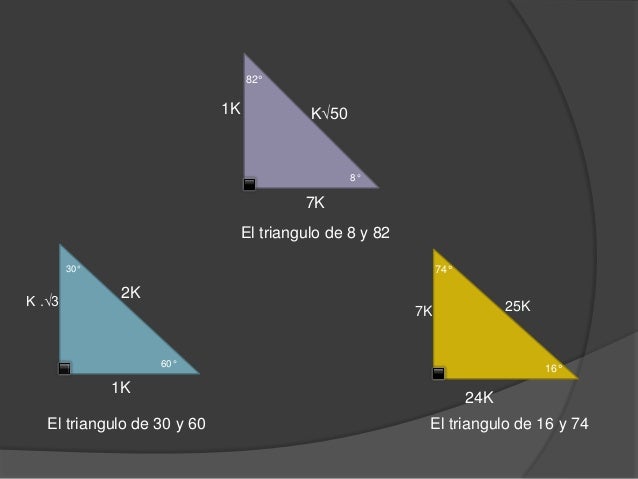



Triangulos Notables
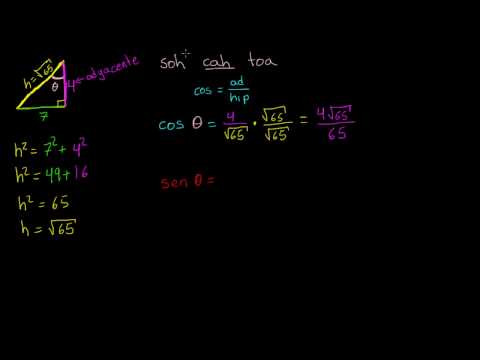



Razones Trigonometricas En Triangulos Rectangulos Video Khan Academy




Funciones Trigonometricas De Los Angulos 30 2 Y 75 Youtube




Unidad I Utilicemos Las Razones Trigonometricas Ppt Descargar
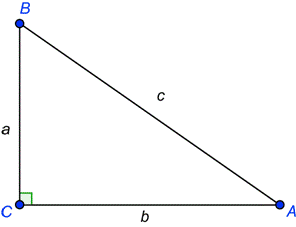



Un Triangulo Rectangulo Tiene Angulos Agudos A Y B Si Y



1
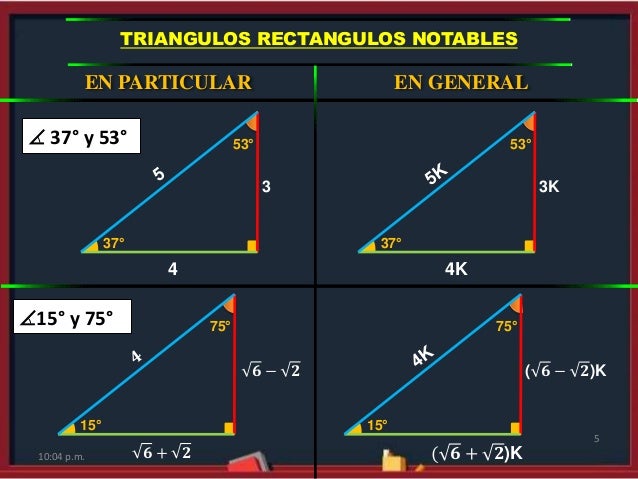



Triangulos Rectangulos Notables



Unidad Vii Geometria Trigonometria Y Series



Www Cbtis136 Edu Mx Public Noticias D167e3c6b532f70ac4f18db11a6a4e90 Pdf




Todo Los Triangulos Notables Sus Angulos Medidas




Seno Coseno Tangente Ck 12 Foundation
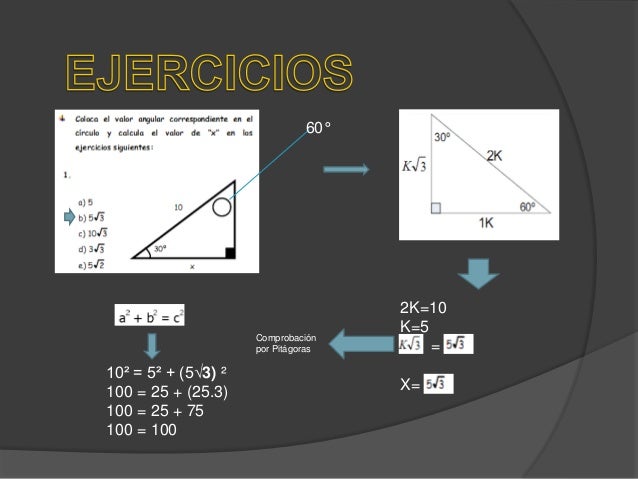



Triangulos Notables




Todo Los Triangulos Notables Sus Angulos Medidas
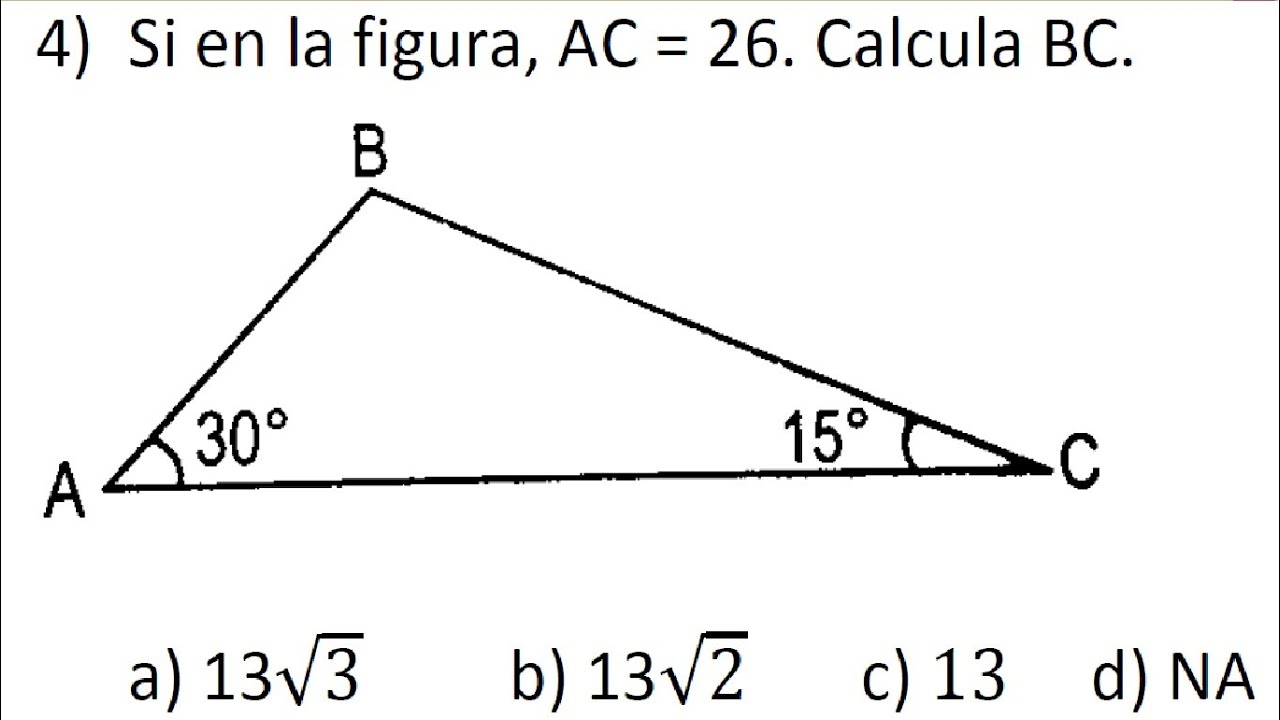



Triangulo Rectangulo Notable 15 Y 75 Youtube



Http Www Juanbragado Es Ficheros Eso Apuntes cuarto eso Repaso Triangulos rectangulos resolucion de problemas Pdf




I Pinimg Com Originals 52 4a 524a45b444cf4




Soluciones Ejercicios
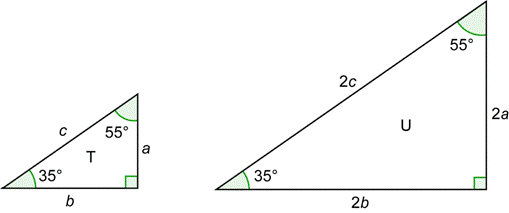



Un Triangulo Rectangulo Tiene Angulos Agudos A Y B Si Y




Seno Coseno Tangente Ck 12 Foundation




Deducir Los Senos Y Los Cosenos




Ley De Los Senos




Triangulos Rectangulos Notables Completo



Www Cbtis136 Edu Mx Public Noticias D167e3c6b532f70ac4f18db11a6a4e90 Pdf




Unidad Iii Funciones Trigonometricas Pdf Free Download



Http Fcaglp Unlp Edu Ar Area Docente Ingreso 14 Modulos 14 Modulo 5 Trigonometria Pdf



0 件のコメント:
コメントを投稿